Jan Created a Piece of Art Shaped Like a Quadrilateral
Geometry
Triangles and Quadrilaterals
Call back / Pair / Share
Follow these directions on your own:
- Draw any triangle on your paper.
- Draw a 2d triangle that is different in some way from your first one. Write down a sentence or two to say how information technology is unlike.
- Draw a 3rd triangle that is different from both of your other two. Draw how it is different.
- Draw 2 more triangles, dissimilar from all the ones that came before.
Compare your triangles and descriptions with a partner. To brand "different" triangles, you have to change some feature of the triangle. Brand a list of the features that you or your partner changed.
Triangles are classified according to dissimilar properties. The point of learning geometry is non to learn a lot of vocabulary, but it's useful to use the correct terms for objects, so that we tin communicate clearly. Here's a quick dictionary of some types of triangles.
Classification by sides
| scalene | isosceles | equilateral |
|---|---|---|
 |  |  |
| all sides have dissimilar lengths | two sides take the aforementioned length | all iii sides accept the aforementioned length |
Classification by angles
| acute | birdbrained |
|---|---|
 |  |
| all interior angles measure less than ninety° | one interior angle measures more than 90 ° |
| right | equiangular |
 |  |
| one interior angle measures exactly 90 ° | all interior angles have the same mensurate |
Remember that "geometry is the art of skilful reasoning from bad drawings." That means you can't ever trust your optics. If y'all look at a picture of a triangle and one side looks similar information technology'south longer than some other, that may but mean the drawing was washed a scrap sloppily.
Notation: Tick marks
Mathematicians either write down measurements or apply tick marks to signal when sides and angles are supposed to be equal.
If ii sides accept the same measurement or the aforementioned number of tick marks, you must believe they are equal and work out the problem accordingly, even if it doesn't look that fashion to your eyes.
You can see examples of these in some of the pictures above. Another example is the little foursquare used to indicate a right bending in the picture of the right triangle.
On Your Own
Piece of work on the post-obit exercises on your own or with a partner.
1. In the moving-picture show below, which sides are understood to accept the same length (even if it doesn't look that way in the drawing)?

two. In the picture show below, which angles are understood to have the same measure (even if if doesn't look that way in the drawing)?

3. Here is a scalene triangle. Sketch two more than scalene triangles, each of which is unlike from the 1 shown here in some manner.

iv. Hither is an acute triangle. Sketch ii more acute triangles, each of which is different from the i shown here in some way.

5. Here is an obtuse triangle. Sketch two more obtuse triangles, each of which is different from the one shown here in some way.

6. Hither is a right triangle. Sketch two more than correct triangles, each of which is dissimilar from the one shown here in some manner. Exist sure to indicate which angle is 90°.

7. Here is an isosceles triangle. Sketch ii more isosceles triangles, each of which is dissimilar from the one shown here in some style. Use tick marks to indicate which sides are equal.

Angle Sum
Recall / Pair / Share
Past now, you have drawn several different triangles on your newspaper. Choose one of your triangles, and follow these directions:
- Using pair of scissors, cut the triangle out.
- Tear (do not cut) off the corners, and place the three vertices together. Your should have something that looks a chip similar this picture:

What exercise yous notice? What does this suggest about the angles in a triangle?
You may recollect learning that the sum of the angles in any triangle is 180°. In your course, you now have lots of examples of triangles where the sum of the angles seems to exist 180°. Only recollect, our drawings are non verbal. How can we be certain that our optics are non deceiving united states? How can we be sure that the sum of the angles in a triangle isn't 181° or 178°, only is really 180° on the nose in every case?
Think / Pair / Share
What would convince yous across all doubt that the sum of the angles in any triangle is 180°? Would testing lots of cases be enough? How many is enough? Could you lot ever test every possible triangle?
History: Euclid'southward axioms
Often high school geometry teachers prove the sum of the angles in a triangle is 180°, usually using some facts near parallel lines. But (maybe surprisingly?) it's but as skilful to accept this every bit an precept, as a given fact near how geometry works, and go from there. Perhaps this is less satisfying than proving it from some other statement, and if you're curious you can certainly notice a proof or your instructor can share one with you.
In about 300BC, Euclid[ane] was the first mathematician (as far as we know) who tried to write down careful axioms and then build from those axioms rigorous proofs of mathematical truths.

Euclid had five axioms for geometry, the get-go iv of which seemed pretty obvious to mathematicians. People felt they were reasonable assumptions from which to build up geometric truths:
one. Given two points, you can connect them with a directly line segment.
ii. Given a line segment, y'all can extend information technology as far every bit you like in either management, making a line.
3. Given a line segment, yous can draw a circle having that segment as a radius.
iv. All right angles are congruent.
The fifth postulate bothered people a flake more. It was originally stated in more than flowery language, merely it was equivalent to this statement:
5. The sum of the angles in a triangle is 180°.
Information technology's easy to meet why this fifth precept caused such a ruckus in mathematics. It seemed much less obvious than the other four, and mathematicians felt like they were somehow cheating if they just assumed it rather than proving information technology had to exist true. Many mathematicians spent many, many years trying to prove this fifth axiom from the other axioms, merely they couldn't practice it. And with good reason: There are other kinds of geometries where the showtime four axioms are true, only the fifth one is not!
For example, if y'all do geometry on a sphere — like a basketball or more importantly on the surface of the Globe — rather than on a flat aeroplane, the first four axioms are true. But triangles are a little foreign on the surface of the earth. Every triangle you tin can draw on the surface of the earth has an angle sum strictly greater than 180°. In fact, yous can draw a triangle on the Earth that has 3 right angles[2], making an bending sum of 270°.
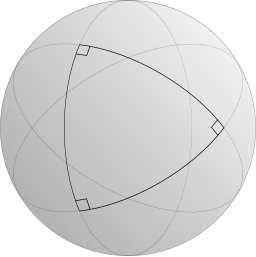
On a sphere like the Earth, the angle sum is non constant amid all triangles. Bigger triangles have bigger angle sums, and smaller triangles have smaller angle sums, but fifty-fifty tiny triangles accept angle sums that are greater than 180°.
The geometry yous study in school is called Euclidean geometry; information technology is the geometry of a flat plane, of a flat world. Information technology's a pretty good approximation for the little piece of the World that we see at any given time, simply information technology's not the only geometry out in that location!
Triangle Inequality
Make a copy of these strips of paper and cut them out. They have lengths from one unit to 6 units. You may want to color the strips, write numbers on them, or do something that makes information technology easy to continue track of the different lengths.

Problem 3
Repeat the following process several times (at least 10) and keep track of the results (a table has been started for you).
- Pick three strips of paper. (The lengths do not have to exist all different from each other; that'due south why y'all have multiple copies of each length.)
- Attempt to brand a triangle with those three strips, and make up one's mind if you think it is possible or not. (Don't overlap the strips, cutting them, or fold them. The length of the strips should be the length of the sides of the triangle.)
| Length ane | Length two | Length 3 | Triangle? |
|---|---|---|---|
| 4 | 3 | 2 | yeah |
| 4 | 2 | 1 | no |
| 4 | two | 2 | ?? |
Your goal is to come up up with a rule that describes when three lengths will make a triangle and when they will not. Write downwardly the rule in your ain words.
Remember / Pair / Share
Compare your rule with other students. And so utilize your rule to answer the following questions. Keep in mind the goal is not to endeavour to build the triangle, but to predict the outcome based on your dominion.
- Suppose you were asked to brand a triangle with sides 40 units, xl units, and 100 units long. Exercise you call up you could do it? Explain your answer.
- Suppose you were asked to make a triangle with sides 2.v units, 2.vi units, and 5 units long. Exercise you call up you could practice information technology? Explain your answer.
Yous probably came up with some version of this statement:
Theorem: Triangle Inequality
The sum of the lengths of 2 sides in a triangle is greater than the length of the tertiary side.
Of course, nosotros know that in geometry we should not believe our eyes. You need to wait for an explanation. Why does your statement make sense?
Remember that "geometry is the art of good reasoning from bad drawings." Our materials weren't very precise, then how can nosotros be sure this rule we've come with is is correct?
Well in this example, the rule is really just the same as the saying "the shortest distance betwixt two points is a straight line." In fact, this is exactly what we mean past the words straight line in geometry.
SSS Congruence
Nosotros say that ii triangles (or any ii geometric objects) are coinciding if they are exactly the aforementioned shape and the same size. That ways that if you could pick one of them upwardly and motility it to put down on the other, they would exactly overlap.
Problem 4
Repeat the post-obit process several times and keep runway of the results.
- Choice three strips of paper that will definitely grade a triangle.
- Endeavour to make two different (non-coinciding) triangles with the same three strips of paper. Tape if you were able to do so.
Problem five
Repeat the following process several times and proceed rails of the results.
- Pick 4 strips of paper and class a quadrilateral with them. (If your four strips exercise not form a quadrilateral, pick some other iv strips.)
- Effort to brand two different (non-coinciding) quadrilaterals with the same 4 strips of newspaper. Record if you were able to do so.
Think / Pair / Share
What practice yous notice from Problems four and v? Tin you brand a general statement to depict what'due south going on? Can you explain why your statement makes sense?
Y'all probably came up with some version of this statement:
Theorem: SSS (side-side-side) Congruence
If two triangles take the same side lengths, and so the triangles are congruent.
This near certainly is not true for quadrilaterals. For instance, if you cull four strips that are however length, you tin can make a square:

Merely yous can also squish that square into a not-square rhombus. (Attempt it!)
If y'all don't choose four lengths that are nevertheless, in improver to "squishing" the shape, you can rearrange the sides to make different (not-congruent) shapes. (Endeavor it!)
 |  |
| These 2 quadrilaterals have the same four side lengths in the same order. | |
|---|---|
 |  |
| These two quadrilaterals have the same four side lengths as the 2 above, but the sides are in a dissimilar society. | |
|---|---|
But this can't happen with triangles. Why not? Well, certainly you can't rearrange the three sides. That would be just the same as rotating the triangle or flipping it over, just not making a new shape.
Why can't the triangles "squish" the way a quadrilateral (and other shapes) tin can? Here's one manner to sympathise it. Imagine you choice two of your iii lengths and lay them on top of each other, hinged at i corner.
| |
| This shows a longer regal dashed segment and a shorter greenish segment. The two segments are hinged at the red dot on the left. |
Now imagine opening upwards the hinge a piffling at a time.
As the swivel opens up, the two not-hinged endpoints go farther and farther apart. Whatever your tertiary length is (bold you are really able to make a triangle with your three lengths), there is exactly i position of the swivel where it will just exactly fit to close off the triangle. No other position will work.
Source: http://pressbooks-dev.oer.hawaii.edu/math111/chapter/triangles-and-quadrilaterals/
0 Response to "Jan Created a Piece of Art Shaped Like a Quadrilateral"
Post a Comment