Odds of Picking a Card and Not Returning and Picking Again
Eugene is a qualified control/instrumentation engineer Bsc (Eng) and has worked as a developer of electronics & software for SCADA systems.
What Is Probability Theory?
Probability theory is an interesting area of statistics concerned with the odds or chances of an event happening in a trial, e.g. getting a half dozen when a dice is thrown or cartoon an ace of hearts from a pack of cards. To work out odds, we as well demand to have an understanding of permutations and combinations. The math isn't terribly complicated, then read on and you lot might be aware!
What's covered in this guide:
- Equations for working out permutations and combinations
- Expectation of an event
- Improver and multiplication laws of probability
- General binomial distribution
- Working out the probability of winning a lottery
Definitions
Before nosotros get started let's review a few cardinal terms.
- Probability is a mensurate of the likelihood of an result occurring.
- A trial is an experiment or test. Due east.yard., throwing a dice or a coin.
- The outcome is the event of a trial. E.grand., the number when a dice is thrown, or the menu pulled from a shuffled pack.
- An consequence is an outcome of interest. E.g., getting a 6 in a dice throw or cartoon an ace.
- Odds is the probability of an event occurring divided by the probability of it not occurring (e.g. one to 5 run a risk of a half-dozen in a dice throw)
What Is the Probability of an Event?
At that place are two types of probability, empirical and classical.
If A is the event of involvement, then we can announce the probability of A occurring as P(A).
Empirical Probability
This is determined past carrying out a series of trials. So, for instance, a batch of products is tested and the number of faulty items is noted plus the number of acceptable items.
If at that place are north trials
and A is the event of interest
Then if event A occurs ten times
P(A) = x / n
Example: A sample of 200 products is tested and 4 faulty items are found. What is the probability of a production being faulty?
So x = 4 and n = 200
Therefore P(faulty item) = four / 200 = 0.02 or 2%
If nosotros exercise the trial once again with a different number of products, nosotros can expect two% of them to be faulty.
Classical Probability
This is a theoretical probability which can be worked out mathematically.
Scroll to Keep
Read More From Owlcation
If A is the outcome, then
P(A) = Number of ways the event tin occur / The full number of possible outcomes
Example i: What are the chances of getting a 6 when a dice is thrown?
In this case, at that place is only 1 mode a 6 can occur and there are 6 possible outcomes, i.e. one, 2, 3, 4, v or half-dozen.
And so P(half dozen) = 1/6
Example 2: What is the probability of drawing a iv from a pack of cards in one trial?
In that location are four ways a 4 can occur, i.e. 4 of hearts, 4 of spades, 4 of diamonds or iv of clubs.
Since in that location are 52 cards, there are 52 possible outcomes in 1 trial.
Then P(4) = 4 / 52 = one / 13
What Is the Expectation of an Outcome?
Once a probability has been worked out, information technology'southward possible to get an estimate of how many events will probable happen in futurity trials. This is known equally the expectation and is denoted past E.
If the event is A and the probability of A occurring is P(A), then for N trials, the expectation is:
E = P(A) N
For the simple example of a dice throw, the probability of getting a six is 1/6.
And so in sixty trials, the expectation or number of expected 6'southward is:
E = one/6 x 60 = x
Recall, the expectation is not what will actually happen, but what is probable to happen. In 2 throws of a dice, the expectation of getting a half-dozen (not 2 sixes) is:
E = one/6 x 2 = i/3
However, as we all know, it's quite possible to go 2 sixes in a row, even though the probability is simply 1 in 36 (see how this is worked out after). Every bit N becomes larger, the actual number of events which happen will become closer to the expectation. So for instance when flipping a coin, if the coin isn't biased, the number of heads will be closely equal to the number of tails.
Success or Failure?
The probability of an event can range from 0 to ane.
Remember
P(Event) = Number of ways the event tin can occur / The total number of possible outcomes
So for a dice throw
P(getting a number betwixt i and half-dozen inclusive) = half dozen / vi = 1 (since at that place are 6 ways you can go "a" number between one and half dozen, and 6 possible outcomes)
P(getting a 7) = 0 / half-dozen = 0 (there are no means the event vii can occur in any of the six possible outcomes)
P(getting a 5) = one / 6 (only i manner of getting a 5)
If at that place are 999 failures in thousand samples
Empirical probability of failure = P(failure) = 999/m = 0.999
A probability of 0 means that an event will never happen.
A probability of one ways that an event will definitely happen.
In a trial, if event A is a success, then failure is non A (not a success)
and:
P(A) + P(not A) = 1
Independent and Dependent Events
Events are independent when the occurrence of one outcome doesn't touch the probability of the other consequence.
So if a card is drawn from a pack, the probability of an ace is 4/52 = 1/xiii.
If the card is replaced, the probability of drawing an ace is nevertheless 1/13.
Two events are dependent if the occurrence of the first event affects the probability of occurrence of the second issue.
If an ace is drawn from a pack and not replaced, there are only 3 aces left and 51 cards remaining, then the probability of drawing a second ace is 3/51.
For ii events A and B where B depends on A, the probability of Result B occurring later on A is denoted by P(B|A).
Mutually Exclusive and Not-Exclusive Events
Mutually exclusive events are events that cannot occur together. For instance in the throwing of a dice, a 5 and a half dozen can't occur together. Another example is picking coloured sweets out of a jar. if an consequence is picking a red sweet, and another event is picking a blue sweet, if a blueish sweet is picked, it can't also be a reddish sweet and vice versa.
Mutually non-exclusive upshots are events that can occur together. For example when a carte is drawn from a pack and the event is a black card or an ace card. If a black is drawn, this doesn't exclude information technology from being an ace. Similarly if an ace is drawn, this doesn't exclude it from beingness a black card.
Addition Law of Probability
Mutually exclusive events
For mutually exclusive (they can't occur simultaneously) events A and B
P(A or B) = P(A) + P(B)
Example one: A sweet jar contains xx crimson sweets, 8 greenish sweets and 10 blueish sweets. If two sweets are pickets are picked out, what is the probability of picking a red or a bluish sweet? (To go on things uncomplicated, the offset sugariness is returned then in that location are nonetheless 38 sweets to cull from when the 2nd sweet is picked)
The event of picking out a red sweet and picking out a blue sweet are mutually sectional.
In that location are 38 sweets in total, so:
P(red) = xx/38 = x/19
P(blue) = 10/38 = 5/xix
P(ruby-red or blue) = P(ruby) + P(blue) = 10/xix + 5/19 = xv/19
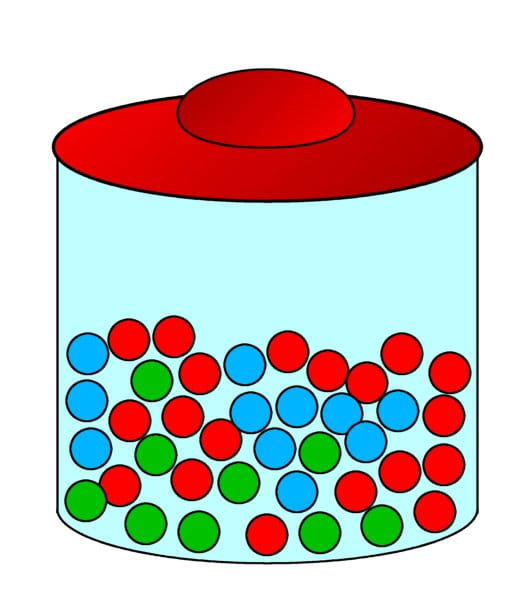
Sweets in a jar
Instance two : A dice is thrown and a card is drawn from a pack, what is the possibility of getting a 6 or an ace?
There is only one way of getting a 6, so:
P(getting a six) is 1/6
At that place are 52 cards in a pack and four ways of getting an ace. Also cartoon an ace is an contained event to getting a 6 (the earlier effect doesn't influence information technology).
P(getting an ace) is 4/52 = 1/13
P(getting a six or an ace) = P(getting a 6) + P(getting an ace)
= ane/half-dozen + 1/13 = (xiii + half-dozen)/78 = 19/78
Remember in these blazon of problems, how the question is phrased is important. So the question was to decide the probability of one event occurring "or" the other event occurring and so the addition law of probability is used.
Mutually non-exclusive events
If two events A and B are mutually non-exclusive, so:
P(A or B) = P(A) + P(B) - P(A and B)
..or alternatively in set theory notation where "U" ways the union of sets A and B and "∩" means the intersection of A and B:
P(A U B) = P(A) + P(B) - P(A ∩ B).
We effectively have to subtract the mutual events that are "double counted". You tin recall of the two probabilities every bit sets and we are removing the intersection of the sets and calculating the marriage of set up A and set B.
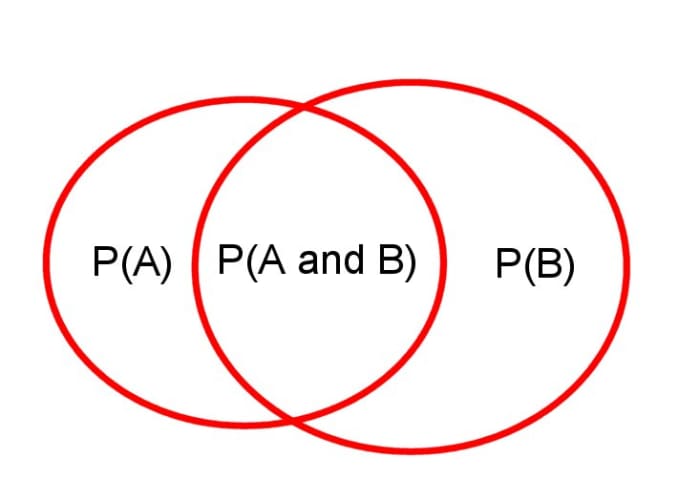
The union of the two sets A and B is P(A U B) = P(A) + P(B) - P(A ∩ B)
© Eugene Brennan
Example three: A coin is flipped twice. Calculate the probability of getting a head in either of the two trials.
In this example we could get a head in one trial, in the second trial or in both trials.
Permit H1 exist the event of a head in the first trial and H2 be the event of a caput in the second trial
P(H1) = 1/two and P(H2) = 1/2 (at that place is only one way a head can occur in each trial and two possible outcomes)
and P(H1 or Hii) = P(H1) + P(Hii) - P(H1 and H2)
There are iv possible outcomes, HH, HT, TH and TT and merely one manner heads can appear twice. So P(H1 and H2) = 1/4
So P(H1 or H2) = P(Hi) + P(Htwo) - P(Hi and H2) = one/2 + i/2 - ane/4 = 3/4
For more than information on mutually non-sectional events, run across this commodity:
Taylor, Courtney. "Probability of the Union of 3 or More Sets." ThoughtCo, February. eleven, 2020, thoughtco.com/probability-union-of-iii-sets-more than-3126263.
Multiplication Police of Probability
For independent (the first trial doesn't affect the 2d trial) events A and B
P(A and B) = P(A) x P(B)
Example: A die is thrown and a bill of fare drawn from a pack, what is the probability of getting a 5 and a spade card?
P(getting a five) = number of ways of getting a 5 / full number of outcomes
= 1/6
At that place are 52 cards in the pack and iv suits or groups of cards, aces, spades, clubs and diamonds. Each suit has xiii cards, so in that location are 13 means of getting a spade.
So P(drawing a spade) = number of means of getting a spade / total number of outcomes
= 13/52 = 1/iv
And so P(getting a 5 and cartoon a spade)
= P(getting a 5) x P(drawing a spade) = 1/6 ten 1/iv = ane/24
Over again information technology'due south important to notation that the give-and-take "and" was used in the question, so the multiplication law was used.
Recommended Books
Engineering science Mathematics by Thousand.A. Stroud is an splendid math textbook for both applied science students and anyone with a general interest in mathematics. The fabric has been written for function 1 of BSc. Engineering Degrees and Higher National Diploma courses.
A wide range of topics are covered including matrices, vectors, complex numbers, calculus, calculus applications, differential equations and series. The text is written in the style of a personal tutor, guiding the reader through the content, posing questions and encouraging them to provide the answer. Personally, I've establish information technology really easy to follow.
It also covers a more than in-depth treatment of probability theory than what has been covered in this commodity plus a section on statistics.
This volume basically makes learning mathematics fun!
Note: 2d manus 1987 editions of this text book are available on Amazon for only virtually $6

Amazon
Summary of Probability Rules
Dominion one:
The probability of an event has a value between 0 and 1 inclusive:
0 ≤ P(A) ≤ 1
Rule ii:
The sum of all probabilities adds upwards to ane
If Ā is the compliment of A, or "non" A, i.east. effect A not occurring, P(Ā) is the probability of A not occurring (or Ā occurring):
P(Ā) + P(A) = ane
Rule 3:
It follows from rule 2 that the probability of an upshot not occurring is 1 - the probability of information technology occurring:
P(Ā) = 1 - P(A)
Rule 4:
For two events A and B:
P(A and B) = P(A) x P(B)
Dominion v:
For mutually exclusive events A and B
P(A or B) = P(A) + P(B)
Rule 6:
For non mutually sectional events:
P(A or B) = P(A) + P(B) - P(A and B)
= P(A) + P(B) - P(A) ten P(B)
Permutations and Combinations
To solve more difficult bug and derive an expression for the probability of a general binomial distribution, nosotros need to empathize the concept of permutations and combinations. I won't go into the mathematics of the derivation, but basically the expression is derived from the equation for working out combinations.
A Permutation Is an Arrangement
A permutation is a way of arranging a number of objects. And then, for instance, if y'all accept the letters A, B, and C so all the possible permutations are:
ABC, ACB, BAC, BCA, CAB, CBA
Notation that BA is a unlike permutation to AB.
If you lot have n objects, there are n factorial number of ways of arranging them, written as n!
north! = due north x (n-i) x (n-2) .... x 3 x two x 1
The reason for this is considering for the get-go position, there are n choices, and for each of these choices, there are (n-1) choices for the 2nd place (because 1 choice was used upward for the starting time place), and for each of the choices in the first two places, (northward-three) choices for the 3rd place and so on.
In the example higher up, the three messages A, B, C could be arranged in three! = three x 2 x 1 = 6 means
In full general, if north objects are selected r at a fourth dimension then, the number of permutations is:
north! / (n-r)!
This is written as nPr
Example: 2 letters are called from the prepare of letters A, B, C, D. How many means can the two letters exist arranged?
There are four letters and so northward =4 and r = 2
nPr = 4Pii = iv! / (4 - 2)! = 4! / two! = iv x iii x ii x 1 / 2 x 1 = 12
A Combination Is a Option
A combination is a fashion of selecting objects from a set without regard to the gild of the objects. So again if we have the letters A, B and C and select three letters from this ready, there is only 1 fashion of doing this, i.e. select ABC.
If we select 2 messages at a time from ABC, all the possible selections are:
AB, Air-conditioning, and BC
Remember, BA is the aforementioned selection equally AB etc.
In general, if yous have n objects in a set and make selections r at a fourth dimension, the total possible number of selections is:
nCr = n! / ((north - r)! r!)
Example: ii letters are chosen from the set ABCD. How many combinations are possible?
There are 4 letters so north = four and r = 2
northCr = 4C2 = four! / ( (4 - 2)! 10 two!) = four! / (2! x 2!)
= 4 x iii x two x 1 / ( (2 x ane) x (2 ten one) ) = 6
General Binomial Distribution
In a trial, an event could be getting heads in a coin throw or a vi in a throw of a dice.
If the occurrence of an event is defined as a success, then
Let the probability of success be denoted by p
Let the probability of non-occurrence of the issue or failure be denoted by q
p + q = i
Permit the number of successes exist r
And northward is the number of trials
Then

Equation for binomial distribution
© Eugene Brennan
Example: What are the chances of getting iii sixes in 10 throws of a dice?
In that location are 10 trials and 3 events of interest, i.eastward. successes and then:
n = 10
r = 3
The probability of getting a 6 in a dice throw is 1/6, so:
p = 1/vi
The probability of non getting a dice throw is:
q = 1 - p = five/6
P(3 successes) = 10! / ((x - 3)! 3!) x (5/6)(10 - 3) x (1/6)3
= ten! / (7! 10 iii!) ten (5/6)7 10 (1/6)3
= 3628800 / (5040 x 6) x (78125 / 279936) x (one/216)
= 0.155
Note that this is the probability of getting exactly three sixes and not whatever more or less.
Winning the Lottery! How to Work out the Odds
We would all like to win the lottery, just the chances of winning are but slightly greater than 0. Nevertheless "If you're not in, you tin can't win" and a slim chance is better than none at all!
Take, for example, the California State Lottery. A histrion must choose 5 numbers betwixt 1 and 69 and one Powerball number between 1 and 26. So that is finer a 5 number selection from 69 numbers and a 1 number selection from 1 to 26. To summate the odds, we need to work out the number of combinations, not permutations, since it doesn't matter what manner the numbers are arranged to win.
The number of combinations of r objects is nCr = n! / ((n - r)! r!)
north = 69
and
r = 5
and
nCr = 69Cfive = 69! / ( (69 - v)! 5!) = 69! / (64! 5!) = 11,238,513
So there are xi,238,513 possible ways of picking 5 numbers from a option of 69 numbers.
Simply 1 Powerball number is picked from 26 choices, so there are only 26 ways of doing this.
For every possible combination of five numbers from the 69, there are 26 possible Powerball numbers, so to get the full number of combinations, we multiply the two combinations.
And so the total possible number of combinations = 11,238,513 ten 26 = 292,201,338 or roughly 293 million and the probability of winning is 1 in 293 meg.
References:
Stroud, Thou.A. (1970). Engineering Mathematics (3rd ed., 1987). Macmillan Education Ltd., London, England.
This article is accurate and true to the best of the writer's cognition. Content is for informational or entertainment purposes only and does non substitute for personal counsel or professional person communication in business, financial, legal, or technical matters.
Questions & Answers
Question: Each Sign has twelve different possibilities, and there are iii signs. What are the odds that whatever two people will share all 3 signs? Note: the signs can be in different aspects, but at the end of the day each person is sharing three signs. For example, one person could have Pisces equally Sun sign, Libra as Rising and Virgo as Moon sign. The other party could have Libra Sunday, Pisces Rising, and Virgo moon.
Answer: In that location are twelve possibilities, and each can have three signs = 36 permutations.
But only half of these are a unique combination (e.g., Pisces and Lord's day is the same as Sunday and Pisces)
so that's eighteen permutations.
The probability of a person getting i of these arrangements is one/18
The probability of ii people sharing all three signs is i/18 ten ane/eighteen = ane/324
Question: I am playing a game with 5 possible outcomes. Information technology is causeless that the outcomes are random. For sake of his argument let us call the outcomes 1, 2, 3, 4 and 5. I have played the game 67 times. My outcomes have been: 1 xviii times, ii nine times, three zero times, four 12 times and 5 28 times. I am very frustrated in non getting a 3. What are the odds of non getting a 3 in 67 tries?
Answer: Since you carried out 67 trials and the number of 3s was 0, and so the empirical probability of getting a iii is 0/67 = 0, so the probability of not getting a 3 is 1 - 0 = 1.
In a greater number of trials there may be an outcome of a 3 so the odds of not getting a 3 would be less than 1.
Question: What if someone challenged yous to never curlicue a 3? If you were to curl the dice eighteen times, what would exist the empirical probability of never getting a three?
Reply: The probability of non getting a 3 is v/6 since there are five ways you lot can not become a 3 and there are half dozen possible outcomes (probability = no. of ways event can occur / no of possible outcomes). In two trials, the probability of not getting a 3 in the first trial AND non getting a 3 in the second trial (emphasis on the "and") would be 5/6 x five/6. In 18 trials, yous keep multiplying 5/6 past 5/six then the probability is (5/half-dozen)^xviii or approximately 0.038.
Question: I have a 12 digit keysafe and would like to know what is the best length to set up to open up iv,5,6 or 7?
Answer: If yous mean setting 4,five,vi or 7 digits for the code, seven digits would of form accept the greatest number of permutations.
Question: If you have 9 outcomes and you need iii specific numbers to win without repeating a number how many combinations would there be?
Answer: It depends on the number of objects due north in a set.
In general, if you accept n objects in a set and make selections r at a time, the total possible number of combinations or selections is:
nCr = northward! / ((northward - r)! r!)
In your case, r is 3
Number of trials is 9
The probability of any particular effect is 1/nCr and the expectation of the number of wins would be one/(nCr) 10 9.
© 2016 Eugene Brennan
Eugene Brennan (author) from Republic of ireland on May 08, 2019:
Not offhand. Yet I did a quick Google search for "games of hazard probability books" and several were listed. Possibly y'all could cheque them out on Amazon and there might be customer reviews.
maurrice on May 08, 2019:
Give thanks you Eugene for this tutorial. Very Interesting! Do y'all recommend whatever book which goes into more item, ideally exploring games of take chances, sports books etc?
Eugene Brennan (author) from Republic of ireland on April 30, 2019:
Hi maurrice,
The probability of the event is 1/half-dozen, so in 60 trials, the probability of that outcome is 1/6 + one/6 + 1/half-dozen....... 60 times.
Information technology's an "or" situation, and then it'due south the probability of that event occurring in trial i or trial 2 or trial three etc up to trial 60.
Then you add the probabilities.
If for instance you throw a dice and the result is getting a vi. Then if the question was "what is the expectation of getting a 6 in each trial", and so you would multiply the probabilities because information technology's an "and" situation.
So information technology'southward the probability of a 6 in trial 1 and a 6 in trial two etc
= one/6 x ane/6, lx times = one/6 ^ 60
In general,
Probability = number of ways result can occur / number of possible outcomes.
So taking the dice example again:
In two trials there's 12 ways yous can become a 6:
ane) 6 in the first trial and 6 other numbers in the second trial (6 possibilities)
2) vi in the second trial and half dozen other numbers in the first trial (6 possibilities)
The number of outcomes is 6 x 6 = 36
Since if yous get 1 in the showtime trial, y'all tin get 1 to 6 in the second trial
If you go 2 in the start trial, y'all can get one to half dozen in the second trial and then on.
So probability = 12/36 = 1/3
So y'all get the same reply as by calculation the probabilities because it's an "or" situation
i/6 + one/6 = 1/3
maurrice on April 29, 2019:
From the following section: What Is the Expectation of an Issue?
Why is the reply calculated every bit 1/half dozen x lx?
Isn't it the aforementioned probability per trial, i.e.:
1st trial = 1/vi chance of getting any number
2nd trial = i/6 chance of getting whatsoever number
and so on...
Therefore, why is it not calculated equally (1/six)^60? What am I missing out/confusing, delight?
Cheers.
Ekki on November 29, 2018:
Cheers so much for this article. It was most helpful. It answered questions that bothered me since the days in college!
Eugene Brennan (author) from Republic of ireland on January 24, 2016:
Thanks Larry!
Larry Rankin from Oklahoma on January 24, 2016:
Wonderful insight into odds.
Eugene Brennan (author) from Ireland on January 21, 2016:
Thanks LM, I learned this stuff in school over 30 years agone, just it was refreshing to revisit it!
LM Gutierrez on Jan 21, 2016:
Thanks for sharing and reiterating the basic mathematics we acquire in our early years of schooling! Actually, this topic is very useful in real life even if you engange in a field which does not deal much on numbers such as mine. I agree with Jodah, well-researched hub!
Eugene Brennan (author) from Ireland on January xviii, 2016:
Thanks Jodah and well spotted! That's what I go for racing through the proof reading!
John Hansen from Gondwana State on January 18, 2016:
It'due south nice to know these equations and the odds of throwing certain numbers of dice, drawing a certain carte du jour etc. Very well researched hub , Eugene. Notwithstanding nether the heading "Probability of an Issue" information technology says; "At that place are two types of probability, empirical and empirical."(should the second one be "classical"?)
Source: https://owlcation.com/stem/How-to-Work-Out-Odds-Permutations-and-Combinations
0 Response to "Odds of Picking a Card and Not Returning and Picking Again"
Post a Comment